java基础算法 二分法查找和基础原理，二分进阶灵活运用练习——小明分巧克力

二分法的时间复杂度是O (logn)，是初学者都需要学的一项最基本算法，下面我们先展示原理在展示代码，然后在进阶练习

原理

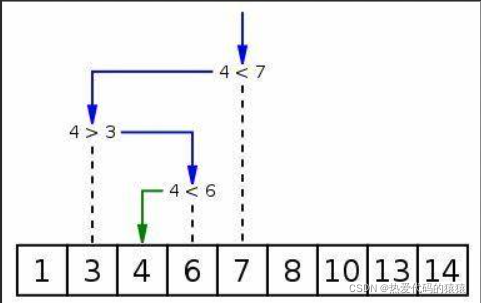
代码：

public class A01_二分法 {
	public int search(int[] nums, int target) {
		int left = 0, right = nums.length - 1;
		int count = 0;
		while (left < right) {
			int mid = (left + right) / 2;
			if (nums[mid] >= target)
				right = mid;
			if (nums[mid] < target)
				left = mid + 1;
		} 
		while (left < nums.length && nums[left++] == target)
			count++;
		return count;
	}
	public static void main(String[] args) {
		A01_二分法 demo = new A01_二分法();
		int a[] = {1,3,4,4,6,7,8,10,13,14};
		System.out.println(demo.search(a,4));
	}
}

基础算法了解了，下面我们来进行一下升级叭！

分巧克力

题目

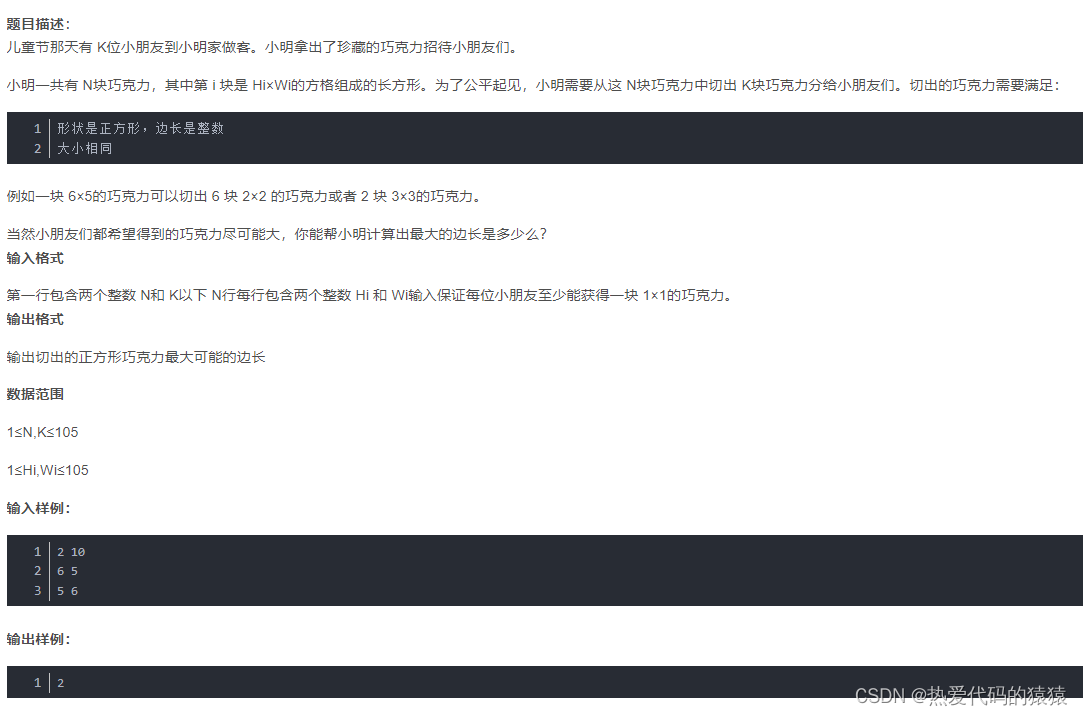
题解难点：

1. 对于一个给定正方形边长x，给定长方形长l、宽w
2. 正方形最多能分割成(l/x)*(w/x)块。
3. 题意要求最小边界为1，最大为巧克力的最大边长
4. 可以复制代码，把注释地方的输出解开，仔细研究一下原理

import java.util.Scanner;

public class 分巧克力 {
    public static void main(String[] args) {
        /**思路分析
         *   n块巧克力分给k位小朋友，设长方形长l,宽w。  分出的相等的正方形巧克力边长x
         *   一个长方形  最多可分l/x * w/x   (w>=x)个巧克力
         *   巧克力与
          */
        Scanner scanner = new Scanner(System.in);
        int n=scanner.nextInt(),k = scanner.nextInt();
        int [][] arr = new int[n][2];
        int max =0;//巧克力最大边长
        for (int i=0;i<n;i++) {
            for (int j=0;j<2;j++) {
                arr[i][j]=scanner.nextInt();
                if (arr[i][j]>=max) {
                    max = arr[i][j];
                }
            }
        }
        //		System.out.println(max);
    //    巧克力最大边长已求出，巧克力最小边长从1开始  用二分法开始累加，直到符合题意==》所有孩子均够分巧克力，且分到的最大
        int l=1,r=max;
        while (l<r){ //l<r,从小到大开始  逐个遍历直到l达到最大值，终止循环,输出l
            int mid = (l+r+1)/2;
            // System.out.println(mid);
            if (judge(arr,k,mid)){
                l=mid;
                // System.out.println("l: "+l);
            }else {
                r=mid-1;
                // System.out.println("r: "+r);
            }
        }
        System.out.println(l);

    }
//    写方法  传入数组，遍历数组，检测是否够孩子分
                                    //arr数组，n巧克力个数，k孩子人数，a每个孩子分到的巧克力边长
    public static boolean judge(int[][]arr,int k,int a) {
        int sum=0;
        for (int i=0;i<arr.length;i++) {
            sum  +=  arr[i][0]/a * arr[i][1]/a;
        }
        if (sum>=k) {
            return true;
        }
        return false;
    }
}